Càlcul infinitesimal

4. PROPOSTA DIDÀCTICA PER A ENSENYAR EL CONCEPTE DE LA DERIVADA A PARTIR DEL QUOCIENT D'INCREMENTS.

"Es pot dir que l'èxit en matemàtiques depèn de la riquesa de les representacions mentals dels conceptes matemàtics; i una representació mental és rica si reflecteix molts aspectes relacionats amb el concepte i si permet passar d'un a l'altre amb facilitat".

Prenent com a referent a Newton i Leibniz amb els seus mètodes per calcular la derivada en un punt i la funció derivada.

La proposta didàctica s'agrupa en quatre seccions:

• Conceptes previs com a velocitat, pendent i quocient incremental.

• Definició de derivada.

• Interpretació geomètrica.

• Regles de derivació.

• Problemes d'aplicació.

4.1.CONCEPTES PREVIS. VELOCITAT, PENDENT I QUOCIENT INCREMENTAL.

4.1.1. Velocitat. Si s'observa el velocímetre d'un automòbil en viatjar al trànsit de la ciutat, es pot veure que l'agulla no roman immòbil molt de temps, és a dir, la velocitat de l'automòbil no és constant. En observar el velocímetre, suposem que el vehicle té una velocitat definida a cada moment, però com es defineix la velocitat?

Apòstol [10] defineix la velocitat mitjana com el quocient entre la diferència de distància a l'interval de temps i l'interval de temps és a dir:

Definint la distància com a f (t) i un interval de temps com l'instant t a l'instant t + h es té:

El nombre h pot ser positiu o negatiu, però no zero. Amb h com a quantitat numèrica infinitament petita es defineix la velocitat instantània per a l'instant t com:

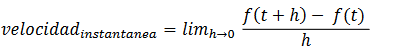
4.1.2. Pendent. Larson [14] Defineix la recta tangent a un punt P en una circumferència com "la recta perpendicular al radi que passa per P figura 6".

 

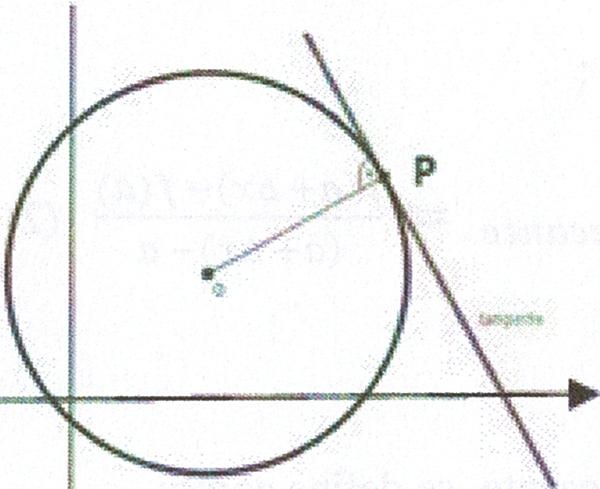
El problema de trobar la recta tangent en un punt P es redueix en calcular-ne el pendent en aquest punt. Aproximar el pendent de la recta tangent usant la recta secant (procedeix del llatí secare que significa tallar) que passa pel punt P i per un altre punt proper de la corba figura 7.

Les fórmules següents s'utilitzen per al càlcul del pendent:

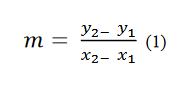
Reemplaçant els punts a (1) :

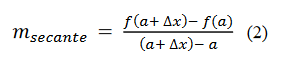
Després el pendent de la recta assecant es defineix com:

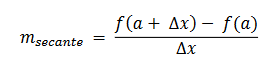
I si hi ha un Ax infinitament petit "que tendeix a zero", llavors el pendent de la recta tangent que passa pel punt de pot calcular com:

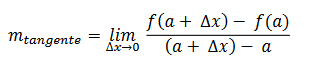
4.1.3. Quocient incremental. Els increments són variacions a les variables. Els increments generalment s'indiquen amb la lletra A. Així Ax és la variació que es produeix a la variable x, és a dir:

I Ay l'increment resultant entre la funció i, és a dir:

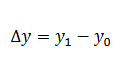
Leibniz utilitza la següent notació per al quocient incremental.

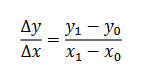
4.2.DEFINICIÓ DE LA DERIVADA A PARTIR DEL QUOCIENT INCREMENTAL

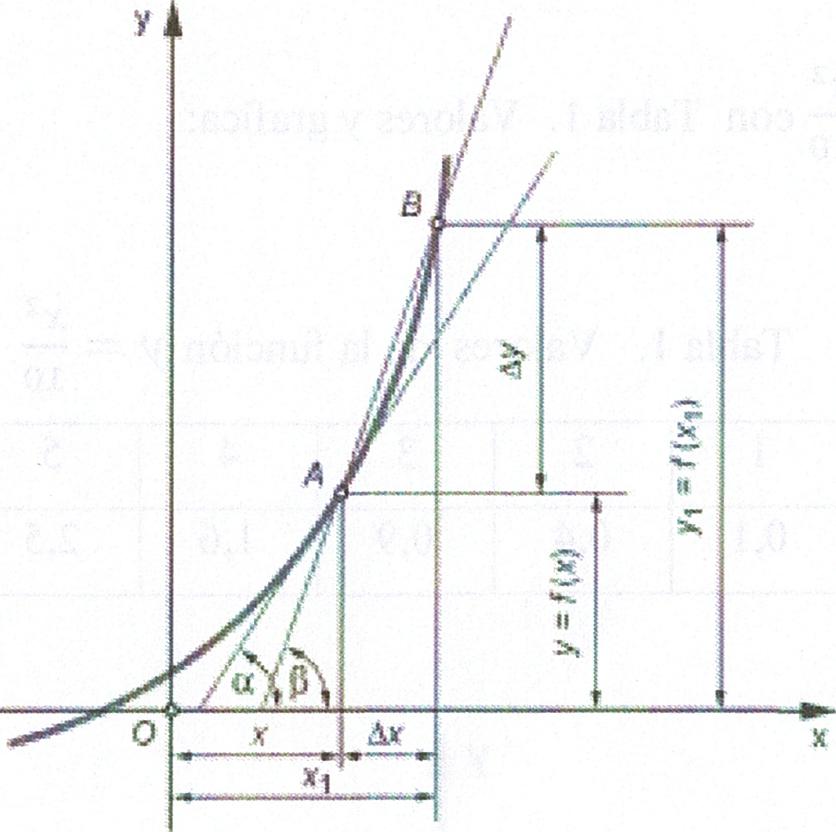
Siga y = f(x) una funció contínua. Si fa variar x la i pot créixer amb x o decréixer, o passar d'un estat decreixent a un altre creixent o viceversa. Com a exemple se suposa la funció y = f(x) creixi amb la x i sigui la seva gràfica la figura 8. Considerant un punt A de la corba amb coordenades (x, y)

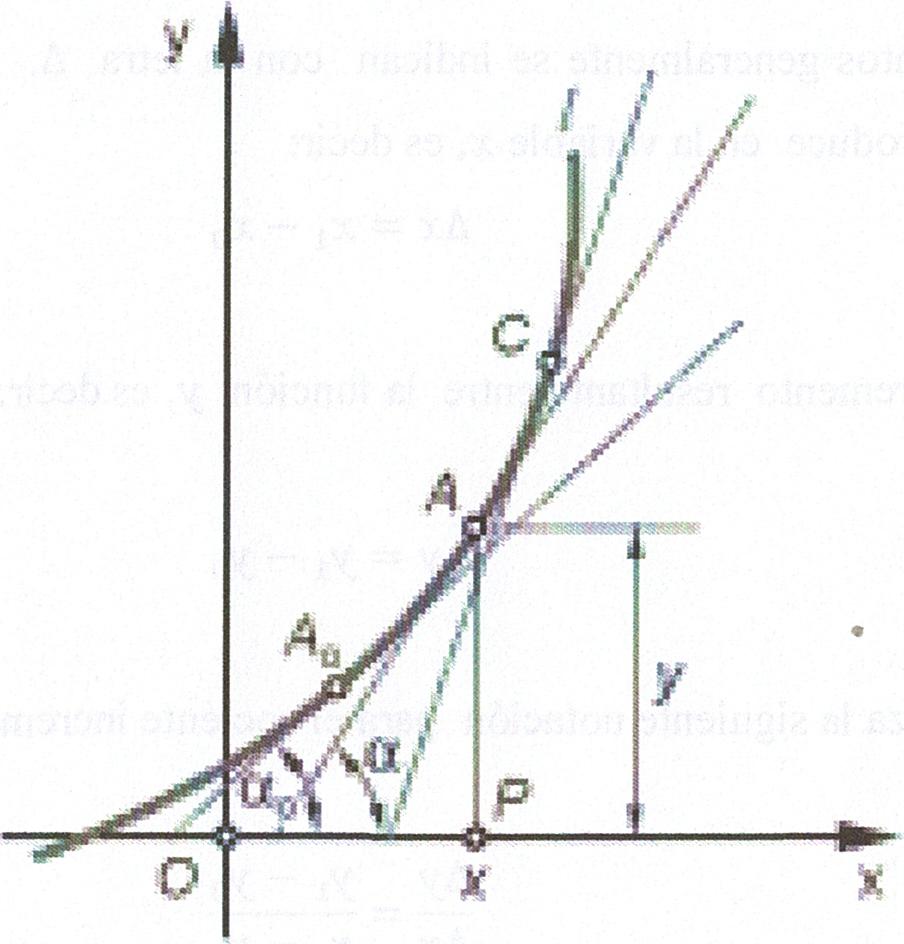
S'observa que per a un determinat increment de x , és més gran l'increment de i com més gran és l'angle al fet que la tangent al punt A. Aleshores el problema es redueix a buscar la tangent a la corba en un punt.

La variable x passa d'un valor x o altre x l , després la funció passarà d'un valor ia un altre

L'increment x 1 — x o s'indicarà amb el símbol Ax després:

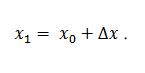
I l'increment i i — i o s'indiqués amb el símbol Ai després

Com i i és el valor que pren la funció per al valor x 1 es pot escriure:

i també

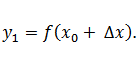
L'increment Ay = Yi — Y o , llavors es pot expressar com:

Ay = f(x + Ax) — f(x)

Dividint tots dos membres per Ax, s'obté:

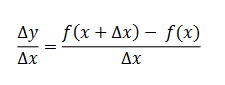
Expressió que rep el nom de quocient incremental de la funció donada. Si Ax tendeix a un nombre infinitesimal petit, el quocient incremental rep el nom de derivada de la funció donada. [6]

Exemple:

Siga y = 2x 2 + 4x. Trobar la derivada:

Utilitzant el quocient incremental i f(x) = 2x 2 + 4x es té:

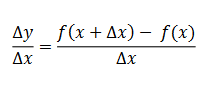
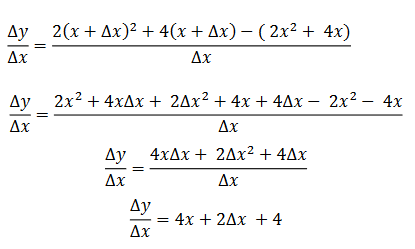
4.3. INTERPRETACIÓ GEOMÈTRICA DEL QUOCIENT INCREMENTAL.

Considerant la gràfica 9 de la funció y = f(x) . Les coordenades del punt A són (x , y) i del punt B són (x1 ,y). Si es darrere l'assecant BA s'observa que:

 

 

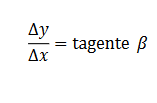
Per tant, el quocient incrementa] de la funció y = f(x) és igual al coeficient angular de la secant que passa per A i per B.

Si Ax és una quantitat infinitament petita, el punt B s'acosta indefinidament al punt A després la secant tendeix a ser la Tangent a A . Després:

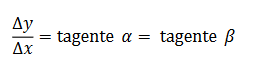
"La derivada d'una funció y = f(x) , en un punt A qualsevol, és la tangent trigonomètrica de l'angle de la tangent que es forma en aquest punt i coneix! eix x" [16]

És a dir:

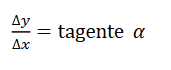
4.4. REGLES DE DERIVACIÓ.

4.4.1. Derivada duna constant. Si una funció és constat, és a dir, sempre conserva el mateix valor de x, l'increment Ay és nul per a qualsevol increment Ax aleshores:

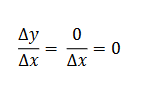
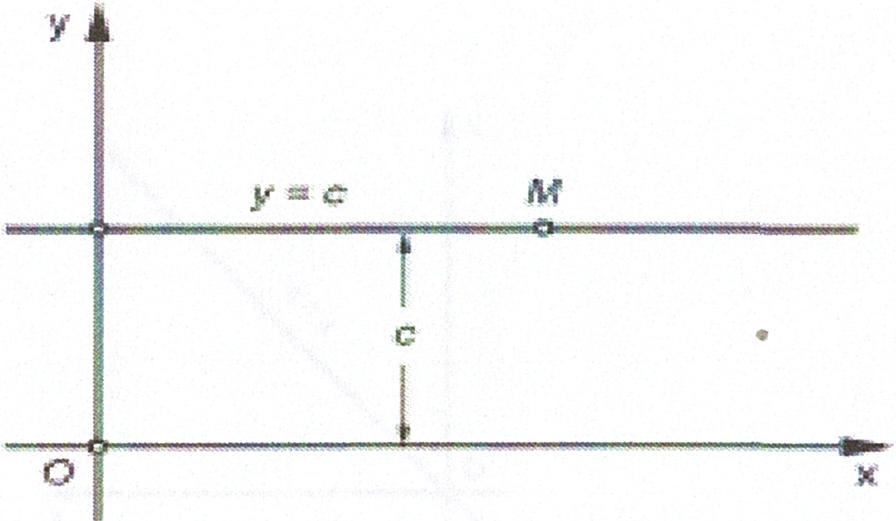
Geomètricament es pot veure la regla ja que la gràfica d'una funció constant f(x) = C ; on C és una constant. És una recta paral·lela a l'eix x, figura 11.

La tangent trigonomètrica de l'angle que es forma entre la recta y = c i l'eix x és zero.

4.4.2. Derivada de la variable independent. Si una funció és constantment igual a la variable independent, la seva expressió és y = x

Per calcular la derivada es té:

Reemplaçant a [1] y = x es té

Dividint [2] entre Ax s'obté:

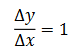
Per tant, la derivada de la variable independent x és 1.

Tertúlies